Das RSA-Debakel: Durch einen Fehler bei der Erzeugung von zufälligen Primzahlen lassen sich die RSA-Schlüssel der TPM-Module von Infinion erraten.
Durch einen Fehler bei der Erzeugung von zufälligen Primzahlen lassen sich die RSA-Schlüssel der TPM-Module von Infinion erraten. Dadurch ist die Sicherheit von Millionen Ausweisen, Computern und Passwortspeichern gefährdet. Der genaue Fehler soll erst in zwei Wochen auf einer Hackerkonferenz veröffentlicht werden, doch es gibt schon jetzt Vorabinformationen zum RSA-Debakel.
Von „RSA“ haben wohl die wenigsten Internetnutzer etwas gehört. Dabei hängt davon in großem Maße die Sicherheit des Internetverkehrs ab. Jeder der heute Onlinebanking betreibt, E-Mails verschickt, in Internetshops kauft oder nur eine https-Webseite aufruft, muss sich auf RSA verlassen können.
RSA-Verschlüsselung verstehen
Jede Verschlüsselung steht vor der Schwierigkeit, zwischen den Kommunikationspartnern einen gemeinsamen Schlüssel auszutauschen, ohne dass er von Dritten abgefangen und mißbraucht werden kann. Dieses Problem hat man in den 1970ern gelöst. Die Trick besteht darin, dass man nicht mehr heimlich, sondern offen einen Teilschlüssel tauscht, mit dem andere die Kommunikation nicht belauschen können. Der Schlüssel wird dazu in einen öffentlichen und einen privaten Teil aufgespalten und als Schlüsselpaar bezeichnet. Man verteilt nur den öffentlichen Schlüssel, der die Nachricht nur verschlüsselt. Den Inhalt wieder lesbar machen kann nur der private Schlüssel. Diesen Schlüssel muss man unbedingt geheim halten. Doch beim RSA-Debakel geht es um etwas anderes.
Das Verfahren wird als asymmetrische Verschlüsselung bezeichnet und ist die Grundlage des RSA-Schlüsselsystems. RSA steht für die Anfangsbuchstaben der Namen der Erfinder Rivest, Shamir und Adleman.
Aufbau des RSA-Schlüssels
Zur Erzeugung einen RSA-Schlüssels benötigt man drei Primzahlen. Die ersten beiden Zahlen p und q sollten möglichst groß und von ähnlicher Länge sein, aber nicht zu dicht beieinander liegen. Die dritte Primzahl hat meistens einen festen Wert von 65537 und wird Verschlüsselungs-Exponent e genannt.
Zur Erzeugung des öffentlichen Schlüssels werden die beiden großen Primzahlen p und v miteinander multipliziert und ergeben den RSA-Modulus n.
n = p · v
e = 65537
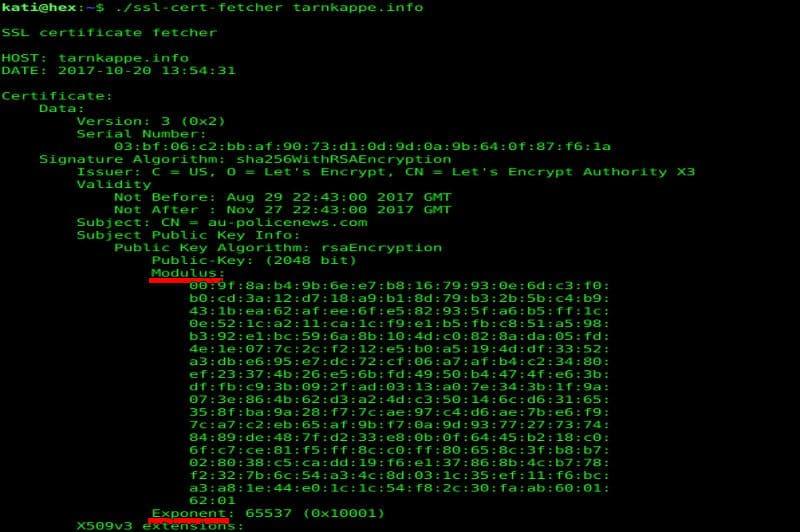
Modulus und Exponent findet man in allen öffentlichen RSA-Schlüsseln (siehe Beitragsbild oben).
Die Sicherheit des öffentlichen Schlüssels beruht darauf, dass es einem Angreifer in absehbarer Zeit nicht gelingt die beiden Komponenten p und v zu erraten oder aus dem Modulus n durch Faktorisierung zu berechnen.
Der private Schlüssel d wird erzeugt, indem zunächst die Eulersche Phi-Funktion φ() des Produktes der beiden Primzahlen berechnet wird. Das ist eine einfache Multiplikation und ergibt eine Zahl, die so lang ist wie beide Primzahlen zusammen.
φ(n) = φ(p·v) = (p-1)·(q-1)
Daraus wird der private Schlüssel d erstellt, der als Entschlüsselungs-Exponent bezeichnet wird, weil er verschlüsselte Nachrichten wieder lesbar macht. d ist das multiplikativ Inverse von e bezüglich des Moduls der Funktion φ(n). Das klingt komplizierter als es ist.
d = e⁻¹ mod φ(n) = 1/e mod (p-1)·(q-1)
d muss man unbedingt geheim halten, während n und e öffentlich zugänglich sind.
RSA-Schlüsselbeispiel
Ein praktisches Beispiel mittels des freien Mathematikprogramms PARI/GP erläutert die Verwendung des Schlüsselpaars. Das Beispiel lässt sich mit der Software auf dem Computer oder diesem Online-Rechner nachvollziehen. (Code in blaues Fenster einfügen und [Evaluate with PARI] starten).:
Code-Beispiel: RSA-Verschlüsselung
Was die jeweiligen Funktionen genau bewirken, lässt sich in der Dokumentation nachschlagen.
Hinweis: Längere Texte muss man in Code-Blöcke block aufbrechen, diese muss man separat verarbeiten. Die Zahl des Buchstabencodes in code muss kleiner sein als die nächste Zweierpotenz lim unterhalb von n: code => block = code % lim ; code = code / lim
Das RSA-Debakel: öffentlichen RSA-Schlüssel knacken
Wer die Primzahlen p und v zu klein wählt (zu kurzer Schlüssel!) bekommt ein Problem, weil sich dann der private Schlüssel aus dem öffentlichen berechnen lässt. Infinion verkauft seit 5 Jahre Chips, deren Firmware fehlerhaft ist und keine zufälligen Primzahlen p und q erzeugt. Die Primzahlen lassen sich erraten.
Hacker verwenden spezielle Verfahren, um den verschlüsselten Code eines schlechten Schlüssels mittels n und e zu knacken. Die Berechnung eines keys kann einige Zeit dauern. Hier sind es nur Bruchteile einer Sekunde:
Code-Beispiel: Mit schwachem RSA-Schlüssel geheimen Code knacken
Es geht sogar noch kürzer nur mit n und e.
text = Strchr(digits(lift(Mod(geheim, n) ^ (1/e % eulerphi(n))), 256))
Der RSA-Schlüssel hat im Beispiel eine Länge von 129 Bit. Das ist mehr als das Doppelte dessen was dem Internet Explorer 5/6 von der US-Regierung für sicheres Bezahlen im Internet erlaubt wurde: 56-bit. Später gab es dann Microsofts High Encryption Pack mit 128 Bit. Solch geringe Verschlüsselung stellt sicher, dass die NSA mitlesen kann… Doch Infineons RSA-Debakel erlaubte der NSA das Knacken der Verschlüsselung.
Tarnkappe.info