Nicht schlecht!
Einer fehlt noch ![]()
Kommt aber auch darauf an wie man kippt, dann würden noch
B,C,D,E in frage kommen
Danach gerhts dabei nur um eine Drehung um 180° !
Aber man kann es wie zur seite kippen oder nach vorne
Wie bei einem blatt Papier
Würde auch sagen
auf den Kopf stellen → BCDE sind dabei NSZ nicht
auf den Kopf drehen → NSZ sind dabei BCDE nicht
Euer Ernst jetzt…?
OK…dem entgegne ich mal:
Text kennzeichnet die optisch dargestellten, alphanumerischen Schriftzeichen einer Nachricht bzw. einer Mitteilung. Ein Text bildet die dargestellte Form der Sprache. Es handelt sich um eine zusammenhängende Information oder Nachricht, die aus den Buchstaben eines Alphabets, aus Ziffern, Interpunktions- und Sonderzeichen bestehen kann.
Nach ISO-Definition handelt es sich bei Text um Informationen für Menschen, die zum besseren Verständnis in zweidimensionaler Form dargestellt werden.
,
Wenn wir also mal nur von den zwei Dimensionen ausgehen, wie es die ISO-Normung vorsieht, wird der Ergebniskreis doch ziemlich eng!
Viele kluge Antworten - schön, wenn bei einer scheinbar simplen Frage eine angeregte Diskussion entsteht ![]()
Nach meiner Definition ist ein Buchstabe/Text etwas Eindimensionales, und wenn man es auf den Kopf stellt, bedeutet das eine Drehung um 180°.
Das hat VIP gemacht und das zunächst fehlende N noch nach geliefert!
Lob und Anerkennung für ihn ![]()
![]()

Xara3d ist ne Schlampe und schreibt sowieso, was du willst! ![]() Aber weil @Tipitester künstlerich so begabt ist, kann er das nächste Rätsel gerne machen!!
Aber weil @Tipitester künstlerich so begabt ist, kann er das nächste Rätsel gerne machen!!
Du bist…
Ich wollte doch eigentlich nur ein bisschen ketzen, aber okay ![]()
Auf meiner Schule waren 763 Schüler. Beweist mir, dass mindestens zwei der Schüler die gleiche Anzahl an Freunden unter den anderen Schülern hatten (nur beidseitige Freundschaften zählen!).
Das läuft auf ein Verfahren hinaus,. das die Mathematiker Schubfachprinzip nennen.
Hier wird’s erklärt - es soll eins der einfachsten Prinzipien der Mathematik sein. Deprimierend, wenn selbst das schon zu hoch für mich ist ![]()
Vielleicht kann einer von euch was damit anfangen.
Ja das ist richtig, aber um das Schubfachprinzip anwenden zu können, muss eine bestimmte Bedingung erfüllt sein. Man muss vorher überlegen, warum diese Bedingung in diesem Fall erfüllt ist.
edit: also das Schubfachprinzip funktioniert folgendermaßen: Man hat eine Gesamtmenge (n), die eine abzählbare Anzahl von Eigenschaften hat (m). Im verlinkten PDF ist im ersten Beispiel als Gesamtmenge 13 Personen angegeben (n=13) und als Eigenschaft der Geburtsmonat (m=12). Wenn man jetzt für jede Eigenschaft ein Schubfach aufstellt, (also 12 Stück von Geburtsmonat 1 bis Geburtsmonat 12) und jede Person einen Stein in das Schubfach wirft, in dem sie Geburtstag hat, müssen mindestens 2 Personen ihren Stein in dasselbe Schubfach werfen, damit ist bewiesen, dass mindestens 2 Personen im selben Monat Geburtstag haben müssen.
Die Bedingung, die erfüllt sein muss, ist also m<n. Wieso ist die im vorliegenden Fall erfüllt?
Wenn ich das Schubladenprinzip mal beiseite lasse, dann ist es bei 763 Personen ja theoretisch möglich, dass 2 Personen mit allen anderen befreundet sind - sie haben dann 762 Freundschaften und sind mit allen (außer sich selbst) wechselseitig befreundet.
Tatsächlich muss man darüber nachdenken was es für Konsequenzen hat, wenn einer der Schüler mit allen anderen Schülern befreundet ist.
Ich weiß nicht, soll ich vielleicht Mal auflösen?
Demnach liege ich mit meinem Lösungsansatz abseits des Schubfachprinzips offensichtlich falsch.
Ich würde für eien Erklärung plädieren, aber möglichst in einfachen klaren Sätzen und nicht mit mathematischen Formeln (Falls man n Objekte auf m Mengen (n,m>0)} verteilt und n größer als m ist, dann gibt es mindestens eine Menge, in der mehr als ein Objekt landet - oder ähnliches) ![]()
Okay, ich versuche es Mal. Also erst noch Mal zu dem pdf das du verlinkt hast:
Wenn 13 Leute ihren Geburtsmonat angeben, müssen mindestens 2 den selben Monat angeben, da es ja nur 12 Monate gibt.
Hier haben wir jetzt 763 Schüler. Dabei kann jeder Schüler maximal mit 762 anderen Schülern befreundet sein, das hast du ja schon gesagt. Es wäre aber auch denkbar, dass jemand 0 andere Freunde hat. Das heißt von 0 bis 762 Freunden ist alles möglich, das wären 763 Antwortmöglichkeiten, also wäre es so weit theoretisch möglich, dass jeder Schüler eine andere Anzahl an Freunden hat.
Der Knackpunkt ist folgender: wenn jemand mit allen anderen Schülern befreundet wäre, gibt es keinen Schüler, der null Freunde haben kann - es zählen ja nur beidseitige Freundschaften. Somit sinkt die Zahl der Antwortmöglichkeiten auf 762, damit müssen bei 763 Schülern mindestens zwei dieselbe Anzahl an Freunden haben.
Ich bin über die Frage gestolpert, als ich nach einer Knobelei für den Thread hier gesucht habe und habe die Antwort leider gesehen, bevor ich selber drüber nachdenken konnte, keine Ahnung ob ich auf die Lösung gekommen wäre, aber ich fand es auch ziemlich tricky.
Wer möchte kann weiter machen!
Gut erklärt! Kann ich verstehen und nachvollziehen - Danke!
Ich hab die Tage auch ein Rätsel entdeckt, was ich für herausfordernd, aber lösbar halte:

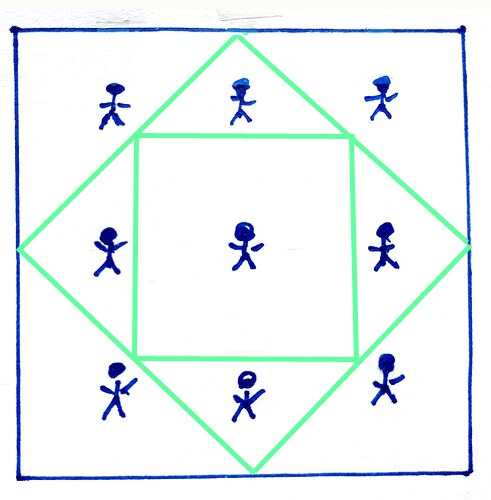
Da ist dieses Quadrat mit den 9 Männchen, das sollst du mit 2 anderen Quadraten so aufteilen, dass jedes Männchen einen Raum für sich alleine hat.
Schade - kein Lösungsversuch ![]()
Dann hier - der Vollständigkeit halber - die Lösung: